C++ Bloom Filter Implementation
A bloom filter is a space efficient data structure which answers the question of “Do you contain this element?” with either “Maybe” or “Definitely not”. Bloom filters trade-off the total confidence of a typical hash set with a huge reduction in memory.
How do they work?
Under the hood a bloom filter is just an array of bits. Initially, all bits are set to 0.
When an item is inserted, it is hashed with K different hash functions.
These hash functions provide K indices into the bit array, which are
all flipped from 0 to 1.
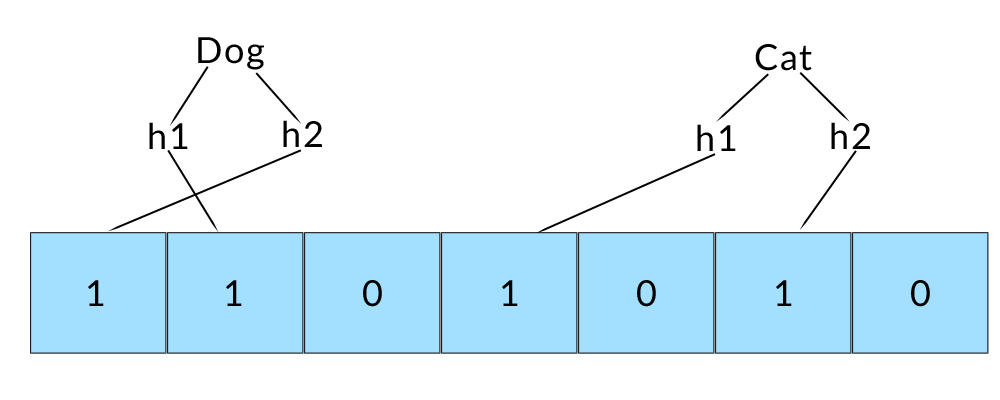
Inserting “Cat” and “Dog” into a bloom filter with
K=2different hash functions.
It then follows that an item is “Maybe” in the bloom filter if for each of its hash indices, the corresponding bit is set to 1. Why only maybe? There is no such thing as the “perfect” hash function, consequently collisions introduce a probability for error.
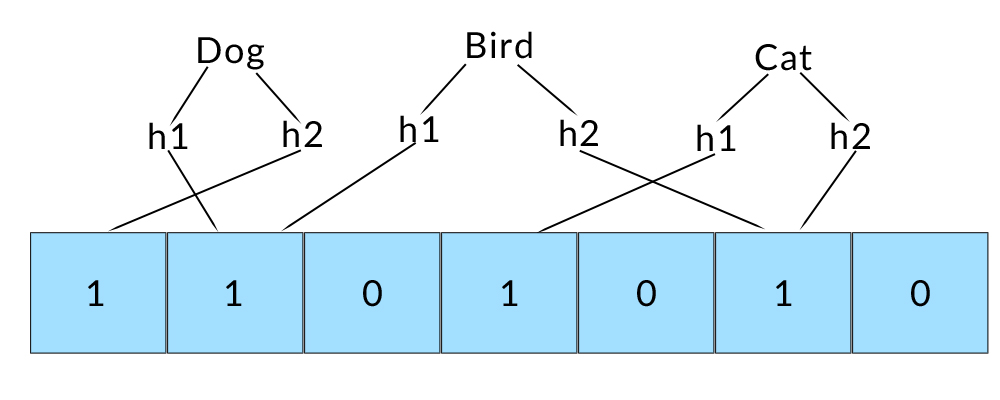
“Bird” collides with other entries. This means that the Bloom filter would identify “Bird” as maybe being a member of the set, when in reality it’s not.
The upside is that if any of the hash indices are 0 for a given element, we can be 100% confident that element is not in the set. This means that Bloom filters can produce false positives but never false negatives.
Memory Savings v.s. a Typical Hash Set
Beware, sketchy math ahead
There is some fancy math on the wikipedia page that states fewer than 10 bits per item is required for a 1% false positive rate. Lets assume we want to store 1,000,000 ASCII strings with an average length of 10 characters.
For a bloom filter this would require:
| 10 bits per element | 10,000,000 bits |
| Total size | 1.19MB |
Note that the actual size of the data does not influence the size of the table.
For a hash set with an 80% occupancy rate this would require:
| 1,200,000 32 bit pointers | 38,400,000 bits |
| 1,000,000 32 bit hash values | 32,000,000 bits | 1,000,000 10 byte strings for collision checking | 80,000,000 bits | </tr>
| Total size | 18.75MB |
The space savings are pretty large if you can afford a 1% margin for error.
Implementation
Bloom filters are pretty straight forward, the one catch is: Where the hell
do we get all these hash functions? In practise it is not feasible to have to
write K hash functions for some potentially large K value.
A commonly used trick is to use a single hash function, and seed a uniform random
generator with the output. This generator can then be used to compute each of the K
“hash values.”