Event Planning
The Problem
Given a set of events, each of which having 0 or more prerequisite events, output a suggested ordering such that all of a given events pre-requisites appear before it.
Data Representation
- Not super intuitive, but a directed graph works very well for this problem
- Directed meaning that edges are not bidirectional
- Each event represents a node in the graph
- An edge going from event A to event B denotes that A is a pre-requisite of B
Building the graph
- We can use a graph structure similar to that in week 2, with a few minor modifications (seen later)
- A full description of this structure can be found here
- Simply read in the end points and connect them on the graph
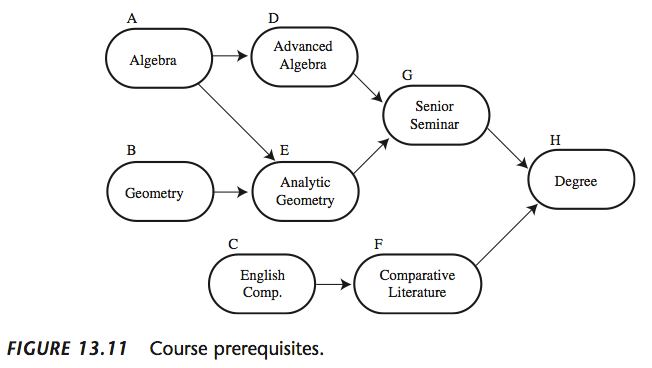
Base Graph (without modifications)
Algorithm for generating sequence
- There is a well known algorithm for sorting graph nodes based on pre-requisites
- Known as topological sort
- Produces a linear ordering of vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering
- Note that this is only possible if the given graph is a DAG (directed acyclic graph)
- Also note that more than 1 valid topological sort may exist for a given DAG
The Algorithm
- The first step is to find all events with no pre-requisites, these will always come first in the ordering
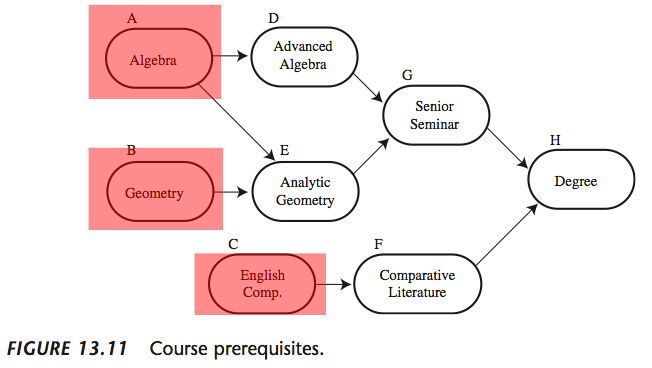
The Algorithm
- We add these events to a queue to be processed, and begin a loop while the queue is not empty
- For each iteration, we pop an element off the queue, and disconnect it from its children
- The reason for this is because it has already been processed, so we are “fulfilling” the pre-requisite
The Algorithm
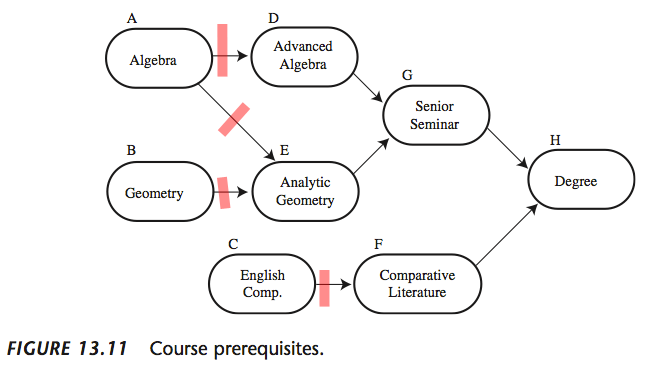
The Algorithm
- We then check if this disconnecting has caused any nodes to have fulfilled pre-requisites
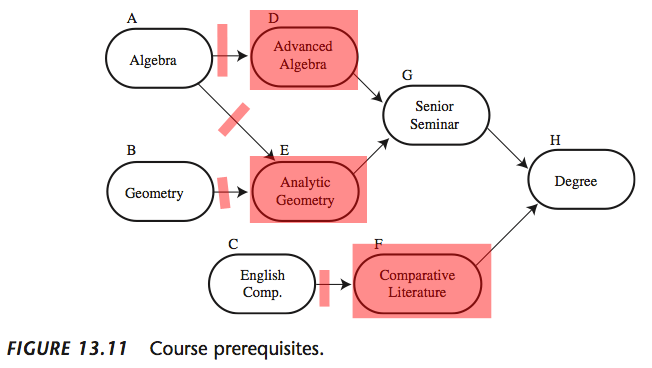
The Algorithm
- Continue this way until we have processed every node in the graph
- At this point we have our ordering
- Our base graph class just needs a way of checking how many incoming edges each node has and we can implement this algorithm