Farmer Kelly
The Problem
Given an M x N matrix of integers, find the sub rectangle such that the sum is maximized.
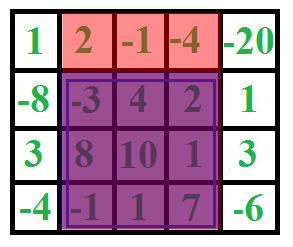
Example
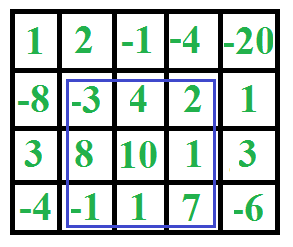
Things to consider
- Negative values may appear in the matrix
- If all values were positive the maximum sum sub rectangle would be the entire matrix
- There is a better solution than checking every sub rectangle
Data representation
- Nothing overly complicated needed
- A 2D array will represent the data exactly as needed
- Usually easier to use a vector<vector<T>> in C++ v.s. T[][] as passing 2D arrays with run time sizes into functions is a little awkward
The Idea
- We can solve the one dimensional version of this problem in linear time using kadanes algorithm
- The rows of the 2D array can be flattened into a 1D array by summing them together
- We can then perform kadanes algorithm on the flattened rows and find the rows bounding the maximum sub sequence
In Action
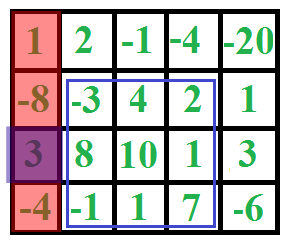
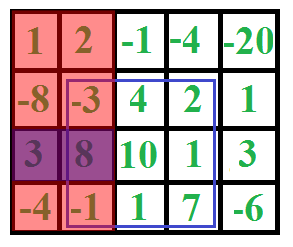
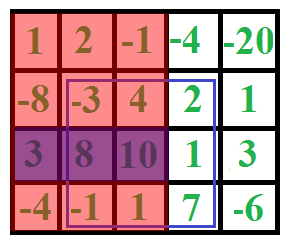
- etc.
One Dimensional Algorithm
- In order to find the row bounds we need to implement the one dimensional maximum sub sequence algorithm
- Known as Kadane’s algorithm, it goes as follows:
- Keep track of the sum of the current prefix that we scanned
- If that prefix ever becomes negative, give up on it and start over
- After each iteration, compare our current prefix sum with the max seen so far and update accordingly
Implementation
Using this algorithm
- To use this algorithm, we simply need to iterate through the matrix fixing the columns
- We can then flatten the elements in between our fixed left and right columns into a one dimensional array
- Once we have our flattened columns, we run the result through kadanes algorithm and recieve the maximum sum as well as the bounding rows