InsertingSpaces
The Problem
You are given a dictionary of words, followed by a list of sentences which have been stripped of all punctuation. You are to determine if spaces can be re-inserted into the sentences such that each word created appears in the given dictionary.
Things to consider
- Words may overlap
- i.e. “cat” and “catch”
- Where you choose to insert the space is important in this case
- This prevents heuristic greedy algorithms
- A word may appear more than once in any sentence
- Test cases are large enough that computing all possible dictionary combinations will eat my CPU
Things to consider
- The key to this problem is finding all valid word prefixes for a given sentence
- Since words may overlap, we must explore each one
Example
- Dictionary:
- cat
- catch
- cha
- Sentence:
- catcha
- You must consider the case of [catch][a] and [cat][cha]
Data Representation
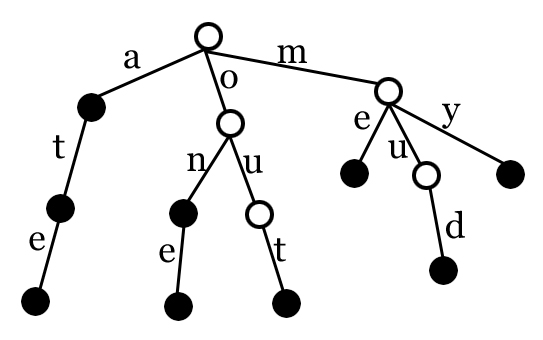
- Since we will be looking for valid word prefixes, this problem lends itself well to the Trie data structure (also known as a prefix tree)
- Trie’s are ordered tree data structures which have the property that all descendants of a given node share a common prefix
- Used commonly for auto-complete and text prediction
Implementation
- Like graphs, most languages do not include a trie structure in the standard library
- Again though, they are easily created using existing data structures
- Each node in the trie contains a map of a Character => TrieNode denoting an out going edge labeled with the character incident on the given TrieNode
- For the purpose of this problem we only need a minimal trie implementation
- insert, and prefixMatches are all that are necessary
- Note that tries can also be used to implement pattern matching i.e.
- find all strings that start with a, followed by any 3 characters, and end with b
- These features are used for things like text prediction and auto complete
Trie Node Implementation
Insert Function
Finding matching prefixes
Putting it all together
- Now that we have a way of finding all valid prefixes, we just have to design an algorithm to solve the problem
- Basically, for each valid prefix we find, we want to remove it from the sentence and then repeat the process with the remaining string
- Once we have exhausted the entire input string, we know that it was a valid sentence
- Seems like a recursive problem