Calculating Coolness
The Problem
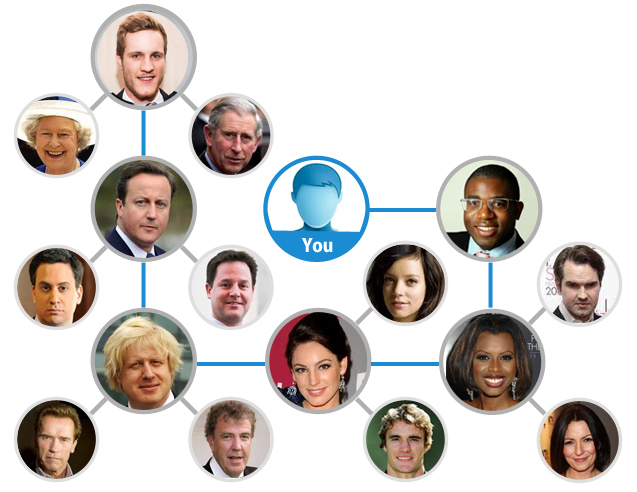
Given a list of friendships, calculate the degrees of separation between each person listed and the coolest guy around Quinn
Step 1: Data Representation
- Often the hardest part of solving any problem
- Very cruicial to the rest of your approach
- Should be well thought out
- The more problems you do, the easier this becomes
Undirected Graphs
- We will represent the data given to us as an undirected graph
- What is a graph?
- Not your typical line or bar graph
- Graphs in math are defined as a 2-tuple (V, E)
- A set of vertices connected by a set of edges
- Each person will be a vertex in our graph and each friendship will be an edge
- Undirected just means that each edge is bidirectional (just like the friendship relation)
Step 2: Choosing an Algorithm
- Now that we have decided on a way to represent our data, we must choose an algorithm to process it
- Since we have decided to use a graph, it would only make sense to consider graph algorithms
Breadth First Search
- Breadth first search is a commonly used algorithm for traversing graphs
- Useful for this problem because it traverses the graph in a level order manner
- It first handles the root (Quinn)
- Then moves to Quinn’s direct neighbours (QDist level 1)
- Continuing down until each level has been processed
Step 3: Implementation
- Now that we have our data structure and algorithm mapped out, we can begin implementing them
Graph Implementation
- Most languages do not include a graph data structure in the standard library
- Thankfully they are relatively simple, and most languages do provide the tools nessesary to do so
- Generally implemented using a map
- We map verticies to a list of their corresponding adjacent verticies
How I Did it
- Not the only way
Breadth First Search and Cycle Detection
- Breadth first search is also relatively easy to implement
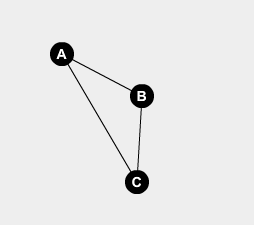
- One thing to keep in mind is that cycles may appear in the graph
- For instance:
Breadth First Search and Cycle Detection
- To handle this we simply need to make sure we do not visit any vertex more than once
- Each time a node is visited add it to a set of visited nodes
- Do not process any node that has already been visited
How I Did It
Putting it all together
- We now have a map that maps each person to their QDist value
- Basically done at this point, we just need to handle the uncool people
- Since there does not exist a path in the graph from them to Quinn, they will not appear in the visited map
- This can be solved many different ways
- You could store all the names at the very beginning and then check which do not appear in the visited map